Linear Regression

Importing packages

We import our standard libraries at this top level.

import numpy as np
import pandas as pd
from matplotlib.pyplot import subplots

New imports

Throughout this lab we will introduce new functions and libraries. However, we will import them here to emphasize these are the new code objects in this lab. Keeping imports near the top of a notebook makes the code more readable, since scanning the first few lines tells us what libraries are used.

import statsmodels.api as sm

We will provide relevant details about the functions below as they are needed.

Besides importing whole modules, it is also possible to import only a few items from a given module. This will help keep the namespace clean. We will use a few specific objects from the statsmodels package which we import here.

from statsmodels.stats.outliers_influence \
     import variance_inflation_factor as VIF
from statsmodels.stats.anova import anova_lm

As one of the import statements above is quite a long line, we inserted a line break \ to ease readability.

We will also use some functions written for the labs in this book in the ISLP package.

from ISLP import load_data
from ISLP.models import (ModelSpec as MS,
                         summarize,
                         poly)

Inspecting Objects and Namespaces

The function dir() provides a list of objects in a namespace.

dir()

['In',
 'MS',
 'Out',
 'VIF',
 '_',
 '__',
 '___',
 '__builtin__',
 '__builtins__',
 '__doc__',
 '__loader__',
 '__name__',
 '__package__',
 '__spec__',
 '_dh',
 '_i',
 '_i1',
 '_i2',
 '_i3',
 '_i4',
 '_i5',
 '_ih',
 '_ii',
 '_iii',
 '_oh',
 'anova_lm',
 'exit',
 'get_ipython',
 'load_data',
 'np',
 'open',
 'pd',
 'poly',
 'quit',
 'sm',
 'subplots',
 'summarize']

This shows you everything that Python can find at the top level. There are certain objects like __builtins__ that contain references to built-in functions like print().

Every python object has its own notion of namespace, also accessible with dir(). This will include both the attributes of the object as well as any methods associated with it. For instance, we see 'sum' in the listing for an array.

A = np.array([3,5,11])
dir(A)

['T',
 '__abs__',
 '__add__',
 '__and__',
 '__array__',
 '__array_finalize__',
 '__array_function__',
 '__array_interface__',
 '__array_prepare__',
 '__array_priority__',
 '__array_struct__',
 '__array_ufunc__',
 '__array_wrap__',
 '__bool__',
 '__buffer__',
 '__class__',
 '__class_getitem__',
 '__complex__',
 '__contains__',
 '__copy__',
 '__deepcopy__',
 '__delattr__',
 '__delitem__',
 '__dir__',
 '__divmod__',
 '__dlpack__',
 '__dlpack_device__',
 '__doc__',
 '__eq__',
 '__float__',
 '__floordiv__',
 '__format__',
 '__ge__',
 '__getattribute__',
 '__getitem__',
 '__getstate__',
 '__gt__',
 '__hash__',
 '__iadd__',
 '__iand__',
 '__ifloordiv__',
 '__ilshift__',
 '__imatmul__',
 '__imod__',
 '__imul__',
 '__index__',
 '__init__',
 '__init_subclass__',
 '__int__',
 '__invert__',
 '__ior__',
 '__ipow__',
 '__irshift__',
 '__isub__',
 '__iter__',
 '__itruediv__',
 '__ixor__',
 '__le__',
 '__len__',
 '__lshift__',
 '__lt__',
 '__matmul__',
 '__mod__',
 '__mul__',
 '__ne__',
 '__neg__',
 '__new__',
 '__or__',
 '__pos__',
 '__pow__',
 '__radd__',
 '__rand__',
 '__rdivmod__',
 '__reduce__',
 '__reduce_ex__',
 '__repr__',
 '__rfloordiv__',
 '__rlshift__',
 '__rmatmul__',
 '__rmod__',
 '__rmul__',
 '__ror__',
 '__rpow__',
 '__rrshift__',
 '__rshift__',
 '__rsub__',
 '__rtruediv__',
 '__rxor__',
 '__setattr__',
 '__setitem__',
 '__setstate__',
 '__sizeof__',
 '__str__',
 '__sub__',
 '__subclasshook__',
 '__truediv__',
 '__xor__',
 'all',
 'any',
 'argmax',
 'argmin',
 'argpartition',
 'argsort',
 'astype',
 'base',
 'byteswap',
 'choose',
 'clip',
 'compress',
 'conj',
 'conjugate',
 'copy',
 'ctypes',
 'cumprod',
 'cumsum',
 'data',
 'diagonal',
 'dot',
 'dtype',
 'dump',
 'dumps',
 'fill',
 'flags',
 'flat',
 'flatten',
 'getfield',
 'imag',
 'item',
 'itemset',
 'itemsize',
 'max',
 'mean',
 'min',
 'nbytes',
 'ndim',
 'newbyteorder',
 'nonzero',
 'partition',
 'prod',
 'ptp',
 'put',
 'ravel',
 'real',
 'repeat',
 'reshape',
 'resize',
 'round',
 'searchsorted',
 'setfield',
 'setflags',
 'shape',
 'size',
 'sort',
 'squeeze',
 'std',
 'strides',
 'sum',
 'swapaxes',
 'take',
 'tobytes',
 'tofile',
 'tolist',
 'tostring',
 'trace',
 'transpose',
 'var',
 'view']

This indicates that the object A.sum exists. In this case it is a method that can be used to compute the sum of the array A as can be seen by typing A.sum?.

A.sum()

19

Simple Linear Regression

In this section we will construct model matrices (also called design matrices) using the ModelSpec() transform from ISLP.models.

We will use the Boston housing data set, which is contained in the ISLP package. The Boston dataset records medv (median house value) for \(506\) neighborhoods around Boston. We will build a regression model to predict medv using \(13\) predictors such as rmvar (average number of rooms per house), age (proportion of owner-occupied units built prior to 1940), and lstat (percent of households with low socioeconomic status). We will use statsmodels for this task, a Python package that implements several commonly used regression methods.

We have included a simple loading function load_data() in the ISLP package:

Boston = load_data("Boston")
Boston.columns

Index(['crim', 'zn', 'indus', 'chas', 'nox', 'rm', 'age', 'dis', 'rad', 'tax',
       'ptratio', 'lstat', 'medv'],
      dtype='object')

Type Boston? to find out more about these data.

We start by using the sm.OLS() function to fit a simple linear regression model. Our response will be medv and lstat will be the single predictor. For this model, we can create the model matrix by hand.

X = pd.DataFrame({'intercept': np.ones(Boston.shape[0]),
                  'lstat': Boston['lstat']})
X[:4]

	intercept	lstat
0	1.0	4.98
1	1.0	9.14
2	1.0	4.03
3	1.0	2.94

We extract the response, and fit the model.

y = Boston['medv']
model = sm.OLS(y, X)
results = model.fit()

Note that sm.OLS() does not fit the model; it specifies the model, and then model.fit() does the actual fitting.

Our ISLP function summarize() produces a simple table of the parameter estimates, their standard errors, t-statistics and p-values. The function takes a single argument, such as the object results returned here by the fit method, and returns such a summary.

summarize(results)

	coef	std err	t	P>|t|
intercept	34.5538	0.563	61.415	0.0
lstat	-0.9500	0.039	-24.528	0.0

Before we describe other methods for working with fitted models, we outline a more useful and general framework for constructing a model matrix~X.

Using Transformations: Fit and Transform

Our model above has a single predictor, and constructing X was straightforward. In practice we often fit models with more than one predictor, typically selected from an array or data frame. We may wish to introduce transformations to the variables before fitting the model, specify interactions between variables, and expand some particular variables into sets of variables (e.g. polynomials). The sklearn package has a particular notion for this type of task: a transform. A transform is an object that is created with some parameters as arguments. The object has two main methods: fit() and transform().

We provide a general approach for specifying models and constructing the model matrix through the transform ModelSpec() in the ISLP library. ModelSpec() (renamed MS() in the preamble) creates a transform object, and then a pair of methods transform() and fit() are used to construct a corresponding model matrix.

We first describe this process for our simple regression model using a single predictor lstat in the Boston data frame, but will use it repeatedly in more complex tasks in this and other labs in this book. In our case the transform is created by the expression design = MS(['lstat']).

The fit() method takes the original array and may do some initial computations on it, as specified in the transform object. For example, it may compute means and standard deviations for centering and scaling. The transform() method applies the fitted transformation to the array of data, and produces the model matrix.

design = MS(['lstat'])
design = design.fit(Boston)
X = design.transform(Boston)
X[:4]

	intercept	lstat
0	1.0	4.98
1	1.0	9.14
2	1.0	4.03
3	1.0	2.94

In this simple case, the fit() method does very little; it simply checks that the variable 'lstat' specified in design exists in Boston. Then transform() constructs the model matrix with two columns: an intercept and the variable lstat.

These two operations can be combined with the fit_transform() method.

design = MS(['lstat'])
X = design.fit_transform(Boston)
X[:4]

	intercept	lstat
0	1.0	4.98
1	1.0	9.14
2	1.0	4.03
3	1.0	2.94

Note that, as in the previous code chunk when the two steps were done separately, the design object is changed as a result of the fit() operation. The power of this pipeline will become clearer when we fit more complex models that involve interactions and transformations.

Let’s return to our fitted regression model. The object results has several methods that can be used for inference. We already presented a function summarize() for showing the essentials of the fit. For a full and somewhat exhaustive summary of the fit, we can use the summary() method.

results.summary()

OLS Regression Results

Dep. Variable:	medv	R-squared:	0.544
Model:	OLS	Adj. R-squared:	0.543
Method:	Least Squares	F-statistic:	601.6
Date:	Tue, 04 Jun 2024	Prob (F-statistic):	5.08e-88
Time:	16:19:08	Log-Likelihood:	-1641.5
No. Observations:	506	AIC:	3287.
Df Residuals:	504	BIC:	3295.
Df Model:	1
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
intercept	34.5538	0.563	61.415	0.000	33.448	35.659
lstat	-0.9500	0.039	-24.528	0.000	-1.026	-0.874

Omnibus:	137.043	Durbin-Watson:	0.892
Prob(Omnibus):	0.000	Jarque-Bera (JB):	291.373
Skew:	1.453	Prob(JB):	5.36e-64
Kurtosis:	5.319	Cond. No.	29.7

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

The fitted coefficients can also be retrieved as the params attribute of results.

results.params

intercept    34.553841
lstat        -0.950049
dtype: float64

The get_prediction() method can be used to obtain predictions, and produce confidence intervals and prediction intervals for the prediction of medv for given values of lstat.

We first create a new data frame, in this case containing only the variable lstat, with the values for this variable at which we wish to make predictions. We then use the transform() method of design to create the corresponding model matrix.

new_df = pd.DataFrame({'lstat':[5, 10, 15]})
newX = design.transform(new_df)
newX

	intercept	lstat
0	1.0	5
1	1.0	10
2	1.0	15

Next we compute the predictions at newX, and view them by extracting the predicted_mean attribute.

new_predictions = results.get_prediction(newX);
new_predictions.predicted_mean

array([29.80359411, 25.05334734, 20.30310057])

We can produce confidence intervals for the predicted values.

new_predictions.conf_int(alpha=0.05)

array([[29.00741194, 30.59977628],
       [24.47413202, 25.63256267],
       [19.73158815, 20.87461299]])

Prediction intervals are computing by setting obs=True:

new_predictions.conf_int(obs=True, alpha=0.05)

array([[17.56567478, 42.04151344],
       [12.82762635, 37.27906833],
       [ 8.0777421 , 32.52845905]])

For instance, the 95% confidence interval associated with an lstat value of 10 is (24.47, 25.63), and the 95% prediction interval is (12.82, 37.28). As expected, the confidence and prediction intervals are centered around the same point (a predicted value of 25.05 for medv when lstat equals 10), but the latter are substantially wider.

Next we will plot medv and lstat using DataFrame.plot.scatter(), \definelongblankMR{plot.scatter()}{plot.slashslashscatter()} and wish to add the regression line to the resulting plot.

Defining Functions

While there is a function within the ISLP package that adds a line to an existing plot, we take this opportunity to define our first function to do so.

def abline(ax, b, m):
    "Add a line with slope m and intercept b to ax"
    xlim = ax.get_xlim()
    ylim = [m * xlim[0] + b, m * xlim[1] + b]
    ax.plot(xlim, ylim)

A few things are illustrated above. First we see the syntax for defining a function: def funcname(...). The function has arguments ax, b, m where ax is an axis object for an exisiting plot, b is the intercept and m is the slope of the desired line. Other plotting options can be passed on to ax.plot by including additional optional arguments as follows:

def abline(ax, b, m, *args, **kwargs):
    "Add a line with slope m and intercept b to ax"
    xlim = ax.get_xlim()
    ylim = [m * xlim[0] + b, m * xlim[1] + b]
    ax.plot(xlim, ylim, *args, **kwargs)

The addition of *args allows any number of non-named arguments to abline, while *kwargs allows any number of named arguments (such as linewidth=3) to abline. In our function, we pass these arguments verbatim to ax.plot above. Readers interested in learning more about functions are referred to the section on defining functions in docs.python.org/tutorial.

Let’s use our new function to add this regression line to a plot of medv vs. lstat.

ax = Boston.plot.scatter('lstat', 'medv')
abline(ax,
       results.params[0],
       results.params[1],
       'r--',
       linewidth=3)

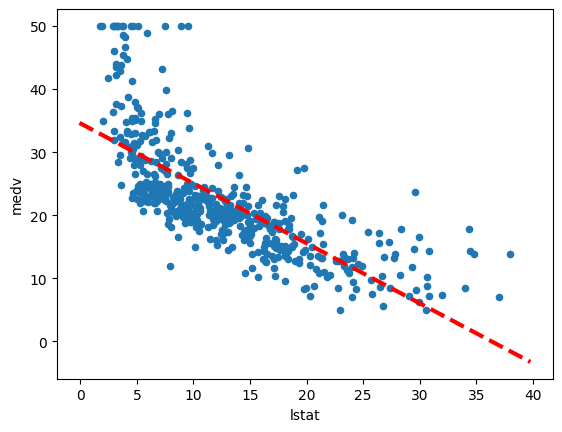
Thus, the final call to ax.plot() is ax.plot(xlim, ylim, 'r--', linewidth=3). We have used the argument 'r--' to produce a red dashed line, and added an argument to make it of width 3. There is some evidence for non-linearity in the relationship between lstat and medv. We will explore this issue later in this lab.

As mentioned above, there is an existing function to add a line to a plot — ax.axline() — but knowing how to write such functions empowers us to create more expressive displays.

Next we examine some diagnostic plots, several of which were discussed in Section~\ref{Ch3:problems.sec}. We can find the fitted values and residuals of the fit as attributes of the results object. Various influence measures describing the regression model are computed with the get_influence() method. As we will not use the fig component returned as the first value from subplots(), we simply capture the second returned value in ax below.

ax = subplots(figsize=(8,8))[1]
ax.scatter(results.fittedvalues, results.resid)
ax.set_xlabel('Fitted value')
ax.set_ylabel('Residual')
ax.axhline(0, c='k', ls='--');

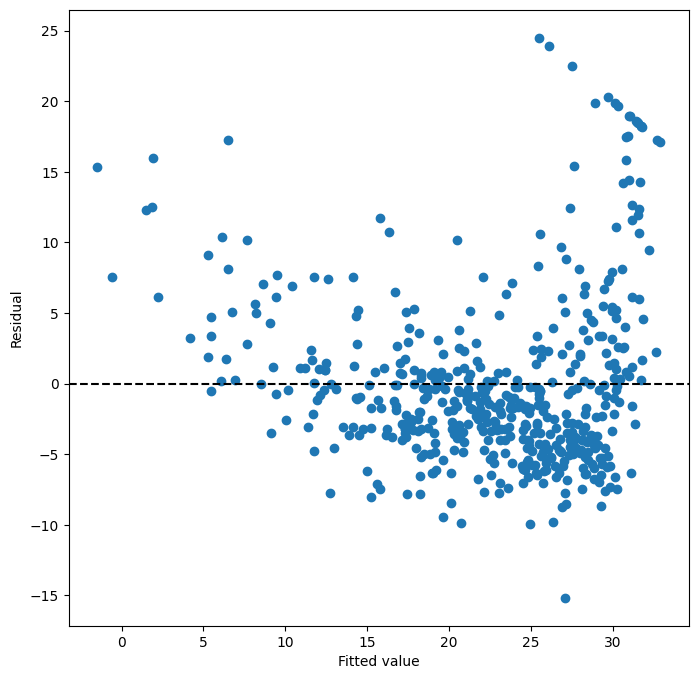
We add a horizontal line at 0 for reference using the ax.axhline() method, indicating it should be black (c='k') and have a dashed linestyle (ls='--').

On the basis of the residual plot, there is some evidence of non-linearity. Leverage statistics can be computed for any number of predictors using the hat_matrix_diag attribute of the value returned by the get_influence() method.

infl = results.get_influence()
ax = subplots(figsize=(8,8))[1]
ax.scatter(np.arange(X.shape[0]), infl.hat_matrix_diag)
ax.set_xlabel('Index')
ax.set_ylabel('Leverage')
np.argmax(infl.hat_matrix_diag)

374

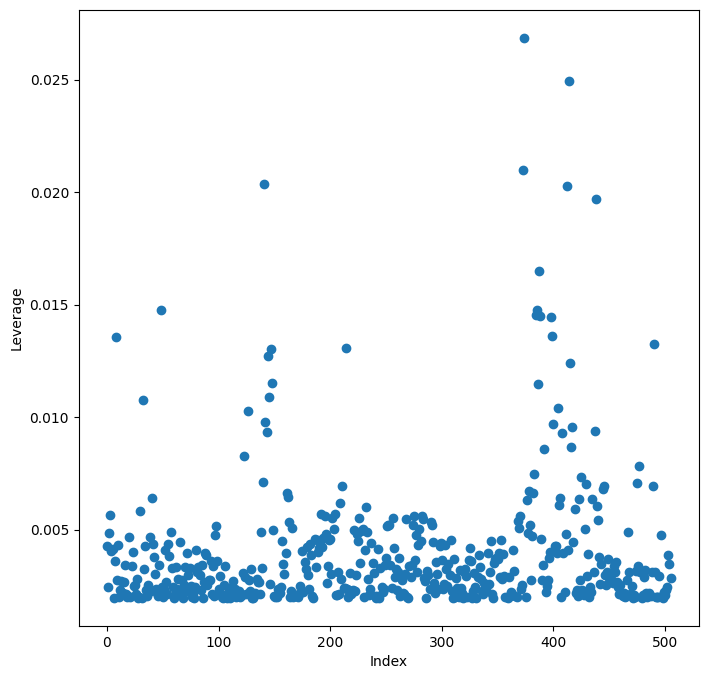
The np.argmax() function identifies the index of the largest element of an array, optionally computed over an axis of the array. In this case, we maximized over the entire array to determine which observation has the largest leverage statistic.

Multiple Linear Regression

In order to fit a multiple linear regression model using least squares, we again use the ModelSpec() transform to construct the required model matrix and response. The arguments to ModelSpec() can be quite general, but in this case a list of column names suffice. We consider a fit here with the two variables lstat and age.

X = MS(['lstat', 'age']).fit_transform(Boston)
model1 = sm.OLS(y, X)
results1 = model1.fit()
summarize(results1)

	coef	std err	t	P>|t|
intercept	33.2228	0.731	45.458	0.000
lstat	-1.0321	0.048	-21.416	0.000
age	0.0345	0.012	2.826	0.005

Notice how we have compacted the first line into a succinct expression describing the construction of X.

The Boston data set contains 12 variables, and so it would be cumbersome to have to type all of these in order to perform a regression using all of the predictors. Instead, we can use the following short-hand:\definelongblankMR{columns.drop()}{columns.slashslashdrop()}

terms = Boston.columns.drop('medv')
terms

Index(['crim', 'zn', 'indus', 'chas', 'nox', 'rm', 'age', 'dis', 'rad', 'tax',
       'ptratio', 'lstat'],
      dtype='object')

We can now fit the model with all the variables in terms using the same model matrix builder.

X = MS(terms).fit_transform(Boston)
model = sm.OLS(y, X)
results = model.fit()
summarize(results)

	coef	std err	t	P>|t|
intercept	41.6173	4.936	8.431	0.000
crim	-0.1214	0.033	-3.678	0.000
zn	0.0470	0.014	3.384	0.001
indus	0.0135	0.062	0.217	0.829
chas	2.8400	0.870	3.264	0.001
nox	-18.7580	3.851	-4.870	0.000
rm	3.6581	0.420	8.705	0.000
age	0.0036	0.013	0.271	0.787
dis	-1.4908	0.202	-7.394	0.000
rad	0.2894	0.067	4.325	0.000
tax	-0.0127	0.004	-3.337	0.001
ptratio	-0.9375	0.132	-7.091	0.000
lstat	-0.5520	0.051	-10.897	0.000

What if we would like to perform a regression using all of the variables but one? For example, in the above regression output, age has a high \(p\)-value. So we may wish to run a regression excluding this predictor. The following syntax results in a regression using all predictors except age.

minus_age = Boston.columns.drop(['medv', 'age']) 
Xma = MS(minus_age).fit_transform(Boston)
model1 = sm.OLS(y, Xma)
summarize(model1.fit())

	coef	std err	t	P>|t|
intercept	41.5251	4.920	8.441	0.000
crim	-0.1214	0.033	-3.683	0.000
zn	0.0465	0.014	3.379	0.001
indus	0.0135	0.062	0.217	0.829
chas	2.8528	0.868	3.287	0.001
nox	-18.4851	3.714	-4.978	0.000
rm	3.6811	0.411	8.951	0.000
dis	-1.5068	0.193	-7.825	0.000
rad	0.2879	0.067	4.322	0.000
tax	-0.0127	0.004	-3.333	0.001
ptratio	-0.9346	0.132	-7.099	0.000
lstat	-0.5474	0.048	-11.483	0.000

Multivariate Goodness of Fit

We can access the individual components of results by name (dir(results) shows us what is available). Hence results.rsquared gives us the \(R^2\), and np.sqrt(results.scale) gives us the RSE.

Variance inflation factors (section~\ref{Ch3:problems.sec}) are sometimes useful to assess the effect of collinearity in the model matrix of a regression model. We will compute the VIFs in our multiple regression fit, and use the opportunity to introduce the idea of list comprehension.

List Comprehension

Often we encounter a sequence of objects which we would like to transform for some other task. Below, we compute the VIF for each feature in our X matrix and produce a data frame whose index agrees with the columns of X. The notion of list comprehension can often make such a task easier.

List comprehensions are simple and powerful ways to form lists of Python objects. The language also supports dictionary and generator comprehension, though these are beyond our scope here. Let’s look at an example. We compute the VIF for each of the variables in the model matrix X, using the function variance_inflation_factor().

vals = [VIF(X, i)
        for i in range(1, X.shape[1])]
vif = pd.DataFrame({'vif':vals},
                   index=X.columns[1:])
vif

	vif
crim	1.767486
zn	2.298459
indus	3.987181
chas	1.071168
nox	4.369093
rm	1.912532
age	3.088232
dis	3.954037
rad	7.445301
tax	9.002158
ptratio	1.797060
lstat	2.870777

The function VIF() takes two arguments: a dataframe or array, and a variable column index. In the code above we call VIF() on the fly for all columns in X.
We have excluded column 0 above (the intercept), which is not of interest. In this case the VIFs are not that exciting.

The object vals above could have been constructed with the following for loop:

vals = []
for i in range(1, X.values.shape[1]):
    vals.append(VIF(X.values, i))

List comprehension allows us to perform such repetitive operations in a more straightforward way.

Interaction Terms

It is easy to include interaction terms in a linear model using ModelSpec(). Including a tuple ("lstat","age") tells the model matrix builder to include an interaction term between lstat and age.

X = MS(['lstat',
        'age',
        ('lstat', 'age')]).fit_transform(Boston)
model2 = sm.OLS(y, X)
summarize(model2.fit())

	coef	std err	t	P>|t|
intercept	36.0885	1.470	24.553	0.000
lstat	-1.3921	0.167	-8.313	0.000
age	-0.0007	0.020	-0.036	0.971
lstat:age	0.0042	0.002	2.244	0.025

Non-linear Transformations of the Predictors

The model matrix builder can include terms beyond just column names and interactions. For instance, the poly() function supplied in ISLP specifies that columns representing polynomial functions of its first argument are added to the model matrix.

X = MS([poly('lstat', degree=2), 'age']).fit_transform(Boston)
model3 = sm.OLS(y, X)
results3 = model3.fit()
summarize(results3)

	coef	std err	t	P>|t|
intercept	17.7151	0.781	22.681	0.0
poly(lstat, degree=2)[0]	-179.2279	6.733	-26.620	0.0
poly(lstat, degree=2)[1]	72.9908	5.482	13.315	0.0
age	0.0703	0.011	6.471	0.0

The effectively zero p-value associated with the quadratic term (i.e. the third row above) suggests that it leads to an improved model.

By default, poly() creates a basis matrix for inclusion in the model matrix whose columns are orthogonal polynomials, which are designed for stable least squares computations. {Actually, poly() is a wrapper for the workhorse and standalone function Poly() that does the work in building the model matrix.} Alternatively, had we included an argument raw=True in the above call to poly(), the basis matrix would consist simply of lstat and lstat**2. Since either of these bases represent quadratic polynomials, the fitted values would not change in this case, just the polynomial coefficients. Also by default, the columns created by poly() do not include an intercept column as that is automatically added by MS().

We use the anova_lm() function to further quantify the extent to which the quadratic fit is superior to the linear fit.

anova_lm(results1, results3)

	df_resid	ssr	df_diff	ss_diff	F	Pr(>F)
0	503.0	19168.128609	0.0	NaN	NaN	NaN
1	502.0	14165.613251	1.0	5002.515357	177.278785	7.468491e-35

Here results1 represents the linear submodel containing predictors lstat and age, while results3 corresponds to the larger model above with a quadratic term in lstat. The anova_lm() function performs a hypothesis test comparing the two models. The null hypothesis is that the quadratic term in the bigger model is not needed, and the alternative hypothesis is that the bigger model is superior. Here the F-statistic is 177.28 and the associated p-value is zero. In this case the F-statistic is the square of the t-statistic for the quadratic term in the linear model summary for results3 — a consequence of the fact that these nested models differ by one degree of freedom. This provides very clear evidence that the quadratic polynomial in lstat improves the linear model. This is not surprising, since earlier we saw evidence for non-linearity in the relationship between medv and lstat.

The function anova_lm() can take more than two nested models as input, in which case it compares every successive pair of models. That also explains why their are NaNs in the first row above, since there is no previous model with which to compare the first.

ax = subplots(figsize=(8,8))[1]
ax.scatter(results3.fittedvalues, results3.resid)
ax.set_xlabel('Fitted value')
ax.set_ylabel('Residual')
ax.axhline(0, c='k', ls='--');

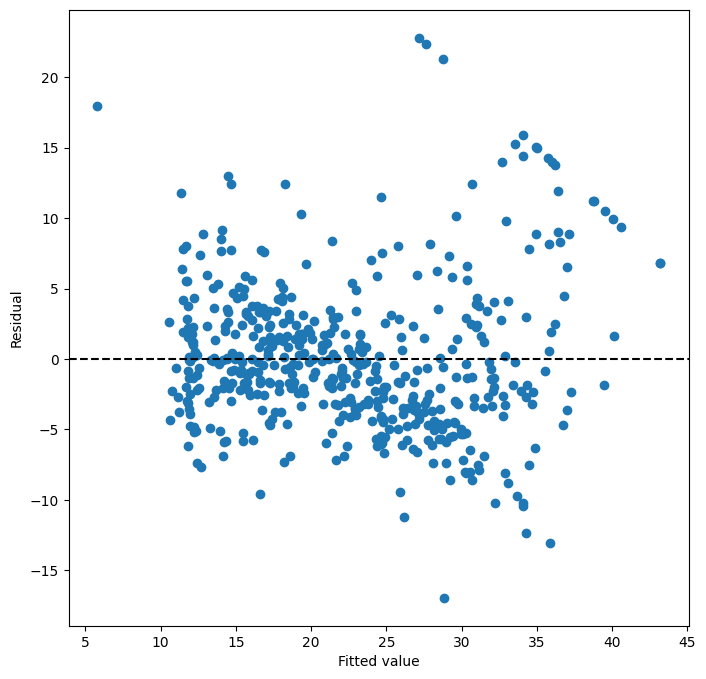
We see that when the quadratic term is included in the model, there is little discernible pattern in the residuals. In order to create a cubic or higher-degree polynomial fit, we can simply change the degree argument to poly().

Qualitative Predictors

Here we use the Carseats data, which is included in the ISLP package. We will attempt to predict Sales (child car seat sales) in 400 locations based on a number of predictors.

Carseats = load_data('Carseats')
Carseats.columns

Index(['Sales', 'CompPrice', 'Income', 'Advertising', 'Population', 'Price',
       'ShelveLoc', 'Age', 'Education', 'Urban', 'US'],
      dtype='object')

The Carseats
data includes qualitative predictors such as ShelveLoc, an indicator of the quality of the shelving location — that is, the space within a store in which the car seat is displayed. The predictor ShelveLoc takes on three possible values, Bad, Medium, and Good. Given a qualitative variable such as ShelveLoc, ModelSpec() generates dummy variables automatically. These variables are often referred to as a one-hot encoding of the categorical feature. Their columns sum to one, so to avoid collinearity with an intercept, the first column is dropped. Below we see the column ShelveLoc[Bad] has been dropped, since Bad is the first level of ShelveLoc. Below we fit a multiple regression model that includes some interaction terms.

allvars = list(Carseats.columns.drop('Sales'))
y = Carseats['Sales']
final = allvars + [('Income', 'Advertising'),
                   ('Price', 'Age')]
X = MS(final).fit_transform(Carseats)
model = sm.OLS(y, X)
summarize(model.fit())

	coef	std err	t	P>|t|
intercept	6.5756	1.009	6.519	0.000
CompPrice	0.0929	0.004	22.567	0.000
Income	0.0109	0.003	4.183	0.000
Advertising	0.0702	0.023	3.107	0.002
Population	0.0002	0.000	0.433	0.665
Price	-0.1008	0.007	-13.549	0.000
ShelveLoc[Good]	4.8487	0.153	31.724	0.000
ShelveLoc[Medium]	1.9533	0.126	15.531	0.000
Age	-0.0579	0.016	-3.633	0.000
Education	-0.0209	0.020	-1.063	0.288
Urban[Yes]	0.1402	0.112	1.247	0.213
US[Yes]	-0.1576	0.149	-1.058	0.291
Income:Advertising	0.0008	0.000	2.698	0.007
Price:Age	0.0001	0.000	0.801	0.424

In the first line above, we made allvars a list, so that we could add the interaction terms two lines down. Our model-matrix builder has created a ShelveLoc[Good] dummy variable that takes on a value of 1 if the shelving location is good, and 0 otherwise. It has also created a ShelveLoc[Medium] dummy variable that equals 1 if the shelving location is medium, and 0 otherwise. A bad shelving location corresponds to a zero for each of the two dummy variables. The fact that the coefficient for ShelveLoc[Good] in the regression output is positive indicates that a good shelving location is associated with high sales (relative to a bad location). And ShelveLoc[Medium] has a smaller positive coefficient, indicating that a medium shelving location leads to higher sales than a bad shelving location, but lower sales than a good shelving location.